Study on the dielectric properties of grass fruit microwave drying process

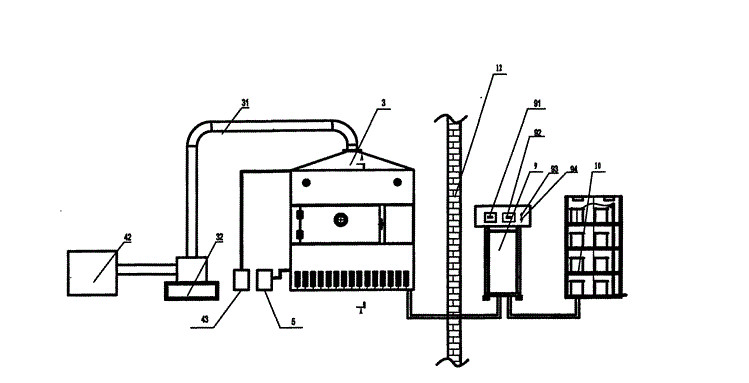
Abstract: The relationship between moisture content and dielectric constant, dielectric loss, loss tangent and penetration depth of grass fruit microwave drying equipment and grass fruit was studied by TG-DTG thermogravimetric analysis and material dielectric parameter test system. The results show that the thermogravimetric process of grass fruit is divided into free water removal stage and bound water removal stage. The dielectric constant and dielectric loss have a trend of gradual decline and sharp decline with the decrease of water content.

When the free water of the grass is present, the dielectric constant and dielectric loss decrease gently. When the grass has only bound water, the dielectric constant and dielectric loss drop sharply. The larger the moisture content of the material, the larger the microwave energy loss and the smaller the penetration depth. On the contrary, the smaller the moisture content of the material, the smaller the microwave energy loss and the greater the penetration depth. The material penetration depth D and the water content ω exist y = Ae- ax + y , which is in exponential relationship.

Key words: grass fruit microwave drying; dielectric properties; penetration depth

The grass fruit is a large-scale Chinese herbal medicine product for both medicine and food. The picking time is from August to December each year, with distinctive characteristics of concentrated picking and regular processing. Due to the high water content of fresh grasses (about 70%), if the dehydration treatment is mildewed, it is necessary to dry and dehydrate the fresh grasses.

At present, the drying of grass fruit mainly includes baking and drying and natural drying of sunlight. Because traditional baking and drying requires strict control of baking temperature and time, drying time is long and drying efficiency is low; while natural sunlight drying is limited by factors such as climate and geographical location, it is easy to be polluted and time consuming. Therefore, it is urgent to find new drying methods that are efficient and low-cost.

As a kind of green heating method, microwave is a material that is heated by in-situ energy conversion inside the material by microwave, and has the characteristics of selective heating and internal heating. Microwave drying of aqueous materials is based on the fact that water can produce intense time-varying polarization in a time-varying microwave field.

The use of these heating advantages of microwaves has the potential to develop new drying methods and processes for grasses. Since the dielectric constant of grass fruit directly determines the ability of grass to absorb microwaves and drying efficiency, it is important to study the dielectric parameters of grasses for microwave drying of grasses.

In this paper, the dielectric dielectric parameter test system is used to study the relationship between the dielectric properties (dielectric constant, dielectric loss, loss tangent and penetration depth) and the moisture content of the material during the drying process of the grass, in order to provide microwave drying for the grass. Theoretical support.

The thermogravimetric process of grass fruit is divided into the free water removal stage and the bound water removal stage. The dielectric constant and dielectric loss have a trend of gradual decline and sharp decline with the decrease of water content. When the water is free, the dielectric constant and dielectric loss decrease gently. When the grass has only bound water, the dielectric constant and dielectric loss drop sharply.

The larger the water content of the material, the larger the microwave energy loss and the smaller the penetration depth. On the contrary, the smaller the water content of the material, the smaller the microwave energy loss and the greater the penetration depth. The material penetration depth D and the water content ω exist y = Ae-ax + y, which is in exponential relationship.